Fig. 1 The Principle of Jet-Dispensing depicted in three steps [Lu et al., 2015, Smart Materials and Structures, 24, 10]
The combination of special jet valves and a well defined feed pressure on the dispensing fluid causes the formation of a so called „jet“ as depicted in Fig. 2. The „jet“ it-self is defined as a droplet flying from the nozzle of the valve to the substrate. The dispensing material is often feeded from a standard cartridge. Regarding the formation of the jet droplet there are two different operation modes:
droplet generating dispensing
jet forming dispensing
The „droplet generating dispensing“ mode is mainly based on a tappet moving within few milliseconds in and out of a seal seat. Below the tappet there is a nozzle with only few hundred mircometers in diameter. During the tappet moves out the feed pressure fills the seal seat with the dispensing fluid. Because of the tappet movement onto the seal seat with a very high velocity, the fluid is push with high pressure through the nozzle. The transfered momentum from the tappet to the fluid works as an additional acceleration force. Thus, beside the feed pressure the tappet stroke, the opening time as well as the closing velocity have similar dependency on the droplet formation [1]. This is why this mode also works at relatively low feed pressures (≥1bar).
Fig. 2 Droplet formation in dependency of the Weber and Ohnesorge number a) We =1 7,4 b) We = 7,9 (no jet) c) On = 1,9 d) On = 0,1 [2]
In contrast, the „jet forming dispensing“ only uses the feed pressure in order to for an elongated droplet named jet. This mode requires a much longer nozzle opening time and higher feed pressure compared to the first one. Moreover, there are also fewer adjustable parameters like closing velocity or tappet stroke [1].
However, the droplet generating dispensing mode is the most used one in micro assembly industry. The reason for this is that this mode allows much smaller dispensing volumes (≤1nl) compared to the jet forming dispensing.
Fig. 3 Dependency of the Weber and Reynolds number on the dispensed droplet form
As depicted in Fig. 3 the droplet or jet formation mainly depends on the a critical Weber number We~c~. The Weber number is a dimensionless number and is defined as the ratio surface tension energy and the kinetic energy of the fluid. Regarding a fluid of density ρ, surface tension σ and viscosity η, which has to be dispensed from a circular shaped nozzle with diameter D with velocity v, the equation describing the Weber number reads:
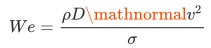
Above the critical Weber number Wec the kinetic energy of the droplet is sufficient to negotiate its surface tension in order to leave the nozzle of the jet valve. If the kinetic energy is too low, the droplet will not reach the fluid breakup regime and stay attached to the nozzle. This mainly occurs for We < We~c~. Low viscosity fluids mainly have a critical Weber number of We~c~=12 [2].
Regarding high viscosity fluids the Ohnesorge number Oh has to be regarded in order to make a decission if the material is suitable for jet dispensing. The Ohnesorge number is defined as ratio between the surface tension energy and the energy which dissipates during the flight phase of the droplet. The Ohnesorge number can be derived from the Weber number We and the Reynolds number Re and is defined as
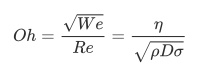
Increasing Ohnesorge numbers are correlated with an increased tendency of stringing. This is mainly influenced by the material parameters dynamic viscosity η, density ρ and surface tension σ as shown by the equation above. Moreover, the required velocity directly correlates with the viscosity.
After the droplet leaves the nozzle its shape ideally is constant in order to reach a defined dispensing result. This behavior is quite complicated to reach and only exist in small parameter ranges. These regimes of deformation of the droplet during the flight phase are depicted in Fig. 3. Figure 3 also depicts that no jet formation occurs below the critical Weber number Wec.
In the range of We~c~ ≤ We ≤ 3We~c~ a jet will be formed but the parts of the droplet will be returned to the nozzle. This is critical for the following dispensing. This behavior can be described by the Rayleigh breakup regime.
Thus, the range of 3We~c~ ≤ We ≤ 4We~c~ might be the optimal range for jet-dispensing within the so called Droplet-on-Demand Regime 2.
For We ≥ 4We~c~ the fluid tends to atomize due to the high velocities. This status is defined as the atomization regime.
[1] T. Lindemann, „Droplet Generation From the Nanoliter to the Femtoliter Range,“ Freiburg i. Br, 2006.
[2] P. K. a. R. Zengerle, „NON-CONTACT NANOLITER & PICOLITER LIQUID DISPENSING,“ University of Freiburg, Freiburg.
[3] L. S. L. Y. Yao Yufeng, „Simulation and Experiment Research of Non-contact Micro-liquid Reagent Dispensing,“ Harbin, 150001, China, 2012.
Um dir ein optimales Erlebnis zu bieten, verwenden wir Technologien wie Cookies, um Geräteinformationen zu speichern und/oder darauf zuzugreifen. Wenn du diesen Technologien zustimmst, können wir Daten wie das Surfverhalten oder eindeutige IDs auf dieser Website verarbeiten. Wenn du deine Zustimmung nicht erteilst oder zurückziehst, können bestimmte Merkmale und Funktionen beeinträchtigt werden.